Figure 1. Plot of function
f_y.derivative function
totalderivative function
Starting with version 2.0, Calcugator has a symbolic toolkit that provides simplification capabilities and symbolic differentiation.
The following basic functions have been implemented:
simplify(f) simplifies function f.
compose(f) expands all function compositions in the definition of function f.
partial(f,s) returns the partial derivative of function f
with respect to the argument name in variable s.
derivative(f) returns the derivative of function f.
totalderivative(f,s) returns the total derivative of function f
with respect to the argument name in variable s.
The following utility functions have been implemented:
gradient(f) returns the gradient of function f in Cartesian
coordinates. Function f maps Rn into R.
jacobian(f) returns the Jacobian of function f in Cartesian
coordinates. Function f maps Rn into Rm.
divergence(f) returns the divergence of function f in Cartesian
coordinates. Function f maps Rn into Rn.
curl(f) returns the curl (rotational) of function f in Cartesian
coordinates. Function f maps R3 into R3.
laplacian(f) returns the Laplacian of function f in Cartesian
coordinates. Function f maps R3 into R.
taylor(f,a,n) returns the Taylor expansion of function f about
point a using up to n derivatives.
Also, functions isDifferentiable, numberOfArguments
and argumentName are useful in the creation of
programs that work with functions.
isDifferentiable(f) returns true if function f is differentiable.
argumentName(f,i) returns the name of the i-th argument of function f.
numberOfArguments(f) returns the number of arguments of function f.
Function simplify(f) simplifies the definition of function f but leaves explicit
function evaluations intact. For instance, assume you have these two functions defined:
Simplifying function f we obtain:
Notice that the simplification of function f left the explicit evaluations
of function g intact. If you need to expand the definition of function g,
use function compose as follows:
The Calcugator language permits the creation of user-defined functions or programs.
Function isDifferentiable(f) returns true only if the following
conditions are met:
f is differentiable in the sense used in standard Calculus.f is done in a single Calcugator statement without using curly brackets.For example, function f below is not differentiable:
The following function is differentiable:
Partial derivatives of differentiable functions can be obtained using function partial.
Function partial(f,s) requires that the call to isDifferentiable(f) returns
true. Variable s must be a string with the name of the argument for which the partial
derivative is being computed.
The computed partial derivative is a full function object. You can evaluate it, plot it, etc.

f_y.The above partial could also be computed as follows:
You could also use function argumentName:
If function f does not depend on a given argument name, function partial returns the
constant function zero.
derivative functionThe derivative function returns the derivative of function f with
respect to its unique argument. Function f must be a function of a single argument.
The statement derivative(f) is equivalent to the
statement partial(f,argumentName(f,1)).
If function f has more than one argument, the call to derivative(f) will
return an error.
Notice that the single quote character (') is a valid Calcugator identifier. You can define variables and function names using single quotes:
totalderivative functionIn standard Calculus, given a function f=f(x,y,t), the total derivative of f with respect to t is defined as follows:
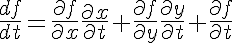
Defining x' as
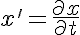
the total derivative is a function of x, y, x', y' and t.
Given a function f=f(x, y, t), Calcugator can compute the total derivative of f using
the function totalderivative.
Notice that Calcugator creates the new arguments x' and y'.
If the function f already has an argument say z', Calcugator assumes it is the derivative with
respect to the given argument. For example, let's assume the position vector of particle is given by
the vector expression p below:
The velocity vector is the total derivative of the position with respect to time:
The acceleration vector is the total derivative of the velocity with respect to time:
The following utilities have been implemented:
The gradient function
Function gradient(f) returns the gradient of function f
in Cartesian coordinates. Function f maps Rn into R.
In standard Calculus the gradient of a function f(x,y,z) is defined as follows:
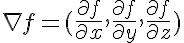
Example:
The jacobian function
Function jacobian(f) returns the Jacobian of function f in
Cartesian coordinates. Function f maps Rn
into Rm.
In standard Calculus the Jacobian of a function f(x,y,z)=(fx(x,y,z), fy(x,y,z), fz(x,y,z)) is defined as follows:
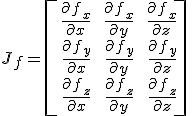
Example:
The divergence function
Function divergence(f) returns the divergence of function
f in Cartesian coordinates. Function f maps
Rn into Rn.
In standard Calculus the divergence of a function f(x,y,z)=(fx(x,y,z), fy(x,y,z), fz(x,y,z)) is defined as follows:
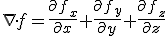
Example:
The curl function
Function curl(f) returns the curl (rotational) of function
f in Cartesian coordinates. Function f maps
R3 into R3.
In standard Calculus the curl of a function f(x,y,z)=(fx(x,y,z), fy(x,y,z), fz(x,y,z)) is defined as follows:
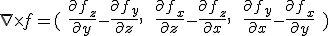
Example:
The laplacian function
Function laplacian(f) returns the Laplacian of function
f in Cartesian coordinates. Function f maps
R3 into R.
In standard Calculus the laplacian of a function f(x,y,z) is defined as follows:
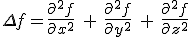
Example:
The taylor function
Function taylor(f,a,n) returns the Taylor expansion of function
f about point a using up to n derivatives.
Function taylor only accepts functions of a single argument.
In standard Calculus the Taylor expansion of a function f(x) at point a is defined as follows:
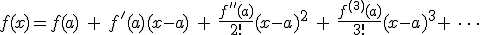
The third argument to function taylor specifies the highest derivative to
be used in the expansion.
Example: